ソラメンバーが学習しているプログラミング言語のひとつに、Processing(プロセッシング)があります。
Processingは、Javaをもとにして作られた、簡単に図を描いたり画像を扱えるようにした言語です。
通常レッスン時に取り組んでいる課題集の中で、「星形を描いてください」というものがあるのですが、この課題、なかなか難しかったりします。
メンバーがこの課題に取り組む段階で得ている知識は、複雑な図形を描くには、
”beginShape(ビギンシェイプ)、vertex(バーテックス)、endShape(エンドシェイプ)という命令を使います。”
”beginShape()で形を描き始め、vertex()で頂点を一つづつ追加してたどっていきます。すべての頂点を追加したら、最後にendShape(CLOSE)で図形を閉じます。”
ということだけ。
描きたい図形の頂点座標を記載すればよいということは、みんなわかるのですが、主に、この課題を取り組んでいるのは小学生達なので、座標の取得方法については様々です。
ペイントで星を描き、座標の値を取得したり、方眼紙から値を取得したり。そもそも課題は星形なので、頂点数が特に指定されているわけではないので、三角形を上下に組み合わせて作品を作るメンバーもいたりします。
でも、星形といえば、五芒星のイメージが強い!結局のところ、ちゃんとした星の座標の求め方って、どうすればいいの?
そんなメンバーの声に、この課題に取り組んでみることにしました。
http://solur.jp/htdocs/star/
ページにアクセスするにはこちら
■ポイント
星を描く方法は色々あると思いますが、今回のポイントは、頂点座標を指定し、図形を描いてみました。
頂点は、外側の円周上にあるもの(偶数番号を振っています)と、内側の円周上にあるもの(奇数番号を振っています)の2種類があることが分かるので、それぞれについて、三角関数を利用し、x軸との角度をθとすれば、円周上の点の座標は(r * cosθ, r * sinθ)と計算することが可能です。
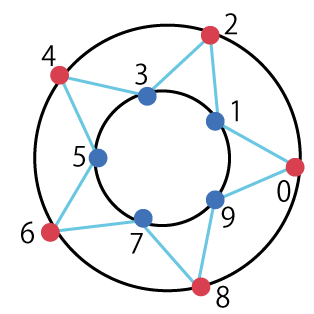
また、頂点番号0の点が上記の位置にあるため、90度回転させます。
結果、以下のようなコードになります。
int n = 10; //頂点数
float R; //半径の変数
float r_out = 150; //外側の円の半径のサイズ
float r_in= r_out * 0.382; //スポーク比の設定
float x;
float y;
void setup(){
size(600,400);
}
void draw(){
pushMatrix();
translate(width/2, height/2); //画面サイズの中心座標に移動
rotate(radians(-90)); //回転する
beginShape();
for (int i = 0; i < n; i++) {
if (i%2 == 0) {
R = r_out; //頂点が偶数の場合
} else {
R = r_in; //頂点が奇数の場合
}
x=(R*cos(radians(360/n * i))); //x座標取得 radians( );ラジアンを度に変換
y=(R*sin(radians(360/n * i))); //y座標取得 radians( );ラジアンを度に変換
vertex(x, y);
}
endShape(CLOSE);
popMatrix();
}
上記を元に色を設定して、ミャンマー連邦の国旗を作ってみました。
いかがでしょうか?
やっぱり、プログラミングって、算数や数学の力が必要だったりしますね。

